Einen Aktien-Index kreieren - Wie funktioniert das?
Im heutigen Blog-Artikel werden verschiedene Aktienindex-Arten sowie das dazugehörige Regelwerk vorgestellt. Im praktischen Teil wird ein nach Freefloat-Marktkapitalisierung gewichteter Index entworfen.
Einleitung
Als Einführung in das Thema wird zuerst ein Index genauer unter die Lupe genommen, welcher nichts mit Aktien zu tun hat. Der Landesindex der Konsumentenpreise (kurz LIK)1 misst die Preisentwicklung anhand eines fix vorgegebenen Warenkorbs. Dieser beinhaltet die wichtigsten, von privaten Haushalten konsumierten Waren und Dienstleistungen. Die Gewichtung der einzelnen Ausgabekategorien sind in der nachfolgenden Grafik ersichtlich:
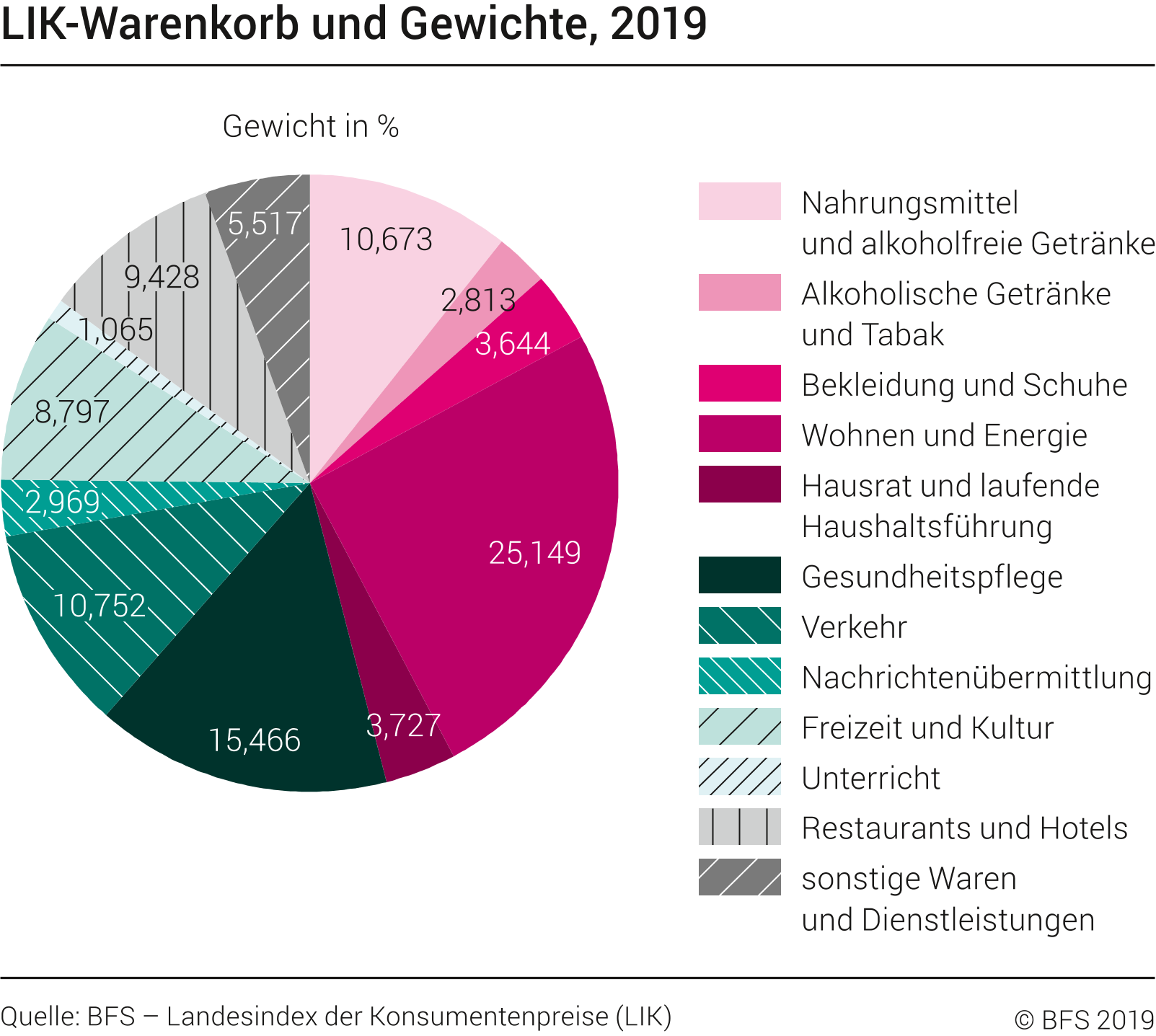
Im Jahre 2015 wurde der Wert des Index $I_t$ auf 100 festgesetzt. Zum Ende jedes Jahres wird nun der Kaufpreis dieses Warenkorbes ermittelt und mit dem Warenwert aus dem Jahr 2015 verglichen. Mit Hilfe der Laspeyres-Formel2 wird der neue Indexwert $I_{t+1}$ berechnet. Ist dieser Wert höher als im Vorjahr ($I_t > I_{t-1}$) wird von einer Teuerung (Inflation) gesprochen, bei einem niedrigen Wert ($I_t < I_{t-1}$) von einer Verbilligung (Deflation).
Bei Aktienindizes sind die einzelnen Komponenten nicht fest vorgegeben, sondern werden mittels eines festgelegten Regelwerkes bestimmt. Die drei Bekanntesten sind:
- Freefloat-Marktkapitalisierungsindex
- Preis-Index
- Faktoren-Index (z.B. Qualität, Momentum, Volatilität)
Freefloat-Marktkapitalisierungsindex
Im restlichen Teil dieses Artikels wird die Bildung eines Freefloat-Marktkapitalisierungindex behandelt.
Komponenten
Um die oben erwähnte Marktkapitalisierung zu erhalten, muss zuerst der Freefloat-Faktor bestimmt werden:
Der Freefloat (Streubesitz) Faktor ist der relative Anteil der Anzahl Aktien, welcher nicht im Festbesitz und somit frei handelbar ist. Bei der Berechnung der Marktkapitalisierung werden in der Regel nur die frei handelbaren Aktien berücksichtigt. Der Freefloat Faktor stellt die frei handelbaren Aktien ins Verhältnis zu der Anzahl Aktien einer Aktienlinie.
Volkswagen hat zum Beispiel nur einen Freefloat Faktor von 10 Prozent, bei Apple sind 85 Prozent der Aktien frei handelbar. Für alle Institutionen im Anlage-Universum kann nun die Freefloat-Marktkapitalisierung berechnet werden:
Die Freefloat Marktkapitalisierung wird durch die Multiplikation des Aktienkurses mit der Anzahl Aktien und dem Freefloat Faktor berechnet. Damit wird die Grösse eines Instruments ausgedrückt.
Nun werden die einzelnen Komponenten mithilfe des berechneten Wertes absteigend sortiert. Danach können diese nach verschiedenen Kriterien ausgewählt werden:
- Fixe Anzahl: Die ersten $n$ Komponenten (z.B. der SMI3 beinhaltet die 30 Schweizer Firmen mit der höchsten Freefloat-Marktkapitalisierung, der S&P 5004 die 500 grössten amerikanischen an der Börse notierten Unternehmen)
- Prozentualer Anteil des Gesamtmarktes: Ein Beispiel dafür sind die Indizes von MSCI (Morgan Stanley Capital International). Diese verwenden folgende Einteilung:
- Large Cap Index: 70% +/- 5%
- Standard Index: 85% +/- 5%
- Investable Market Index (IMI): 99% +1% oder -0.5%
Indexwert
Nun sind die Bestandteile des Index bestimmt und am Ende jedes Handelstages kann nun der Wert des Index ($I$) zum Zeitpunkt $t$ ermittelt werden:
$$
I_t = {M_t \over D_t} = {\sum_{i=1}^n s_{i,t}f_{i,t}c_{i,t}p_{i,t}x_{i,t} \over D_t}
$$
Die Formel setzt sich aus folgenden Variablen zusammen:
- Marktwert ($M$)
- Zeitpunkt ($t$)
- Anzahl Aktien ($s$)
- Freefloat Faktor ($f$)
- Kappungsfaktor ($c$)
- Preis ($p$)
- Umrechnungskurs ($x$)
- Spezifische Indexkomponente ($i$)
- Anzahl Indexkomponenten ($n$)
Die Indexbasis wird bei der Erstellung eines Index festgelegt. Beim LKI wurde ein Wert von 100 festgesetzt, beim SMI einer von 1’500 (30. Juni 1988). Dafür wird ein sogenannter Divisor ($D$) benötigt. In den Dokumenten von SIX wird dieser so beschrieben:
Der Divisor hat zwei Daseinsberechtigungen. Einerseits wird er dazu verwendet den Indexwert zu Beginn des Index auf eine sinnvolle Grösse zu standardisieren. Der Divisor wird ab dem Tag fortgeschrieben, an dem der Basiswert des Index bestimmt wurde. Andererseits wird er während der gesamten Laufzeit des Index dazu genutzt, um externe Effekte auszugleichen, die zu einer potentiell täglichen Änderung im Marktwert ($\Delta M$) führen können. Diese Effekte haben normalerweise die Form von Corporate Actions (Kapitalereignisse) und ein definiertes Effektivdatum. Daher wird der Divisor täglich angepasst und innerhalb eines Tages konstant gehalten. Berechnet wird der neue Divisor am Abend des Tages bevor die Corporate Action effektiv wird.
Beispiele für Kapitalereignisse sind Dividendenzahlungen oder Aktien-Splits. Um die nachfolgenden Berechnung zu vereinfachen, wird angenommen, dass der zu Beginn festgelegte Divisor konstant bleibt (keine externe Einflüsse).
Ein einfaches Beispiel für die Berechnung des Indexwertes mit einer Feststellung von 1’500 Punkten und einem Divisor von 100:
| $t$ | $D$ | $M$ | $\Delta M$ | $I$ |
|---|---|---|---|---|
| 0 | 100 | 150’000 | 1’500 | |
| 1 | 100 | 150’150 | 150 | 1’501.5 |
| 2 | 100 | 149’700 | -450 | 1’497 |
| 3 | 100 | 149’295 | -405 | 1’492.95 |
| 4 | 100 | 150’495 | 1’200 | 1’504.95 |
Kappungsfaktor
Ein Kappungsfaktor ($c$) wird benutzt, um das Gewicht einer Indexkomponente im Index zu limitieren. Dieser Faktor wird mithilfe des aktuellen Gewichtes sowie dem maximalen Gewicht im Index berechnet. So wird zum Beispiel die Firma Nestlé (ca. ein Gewicht $g_{ist}$ von 18% im SMI) im SLI (Swiss Leader Index) nach ca. 9 Prozent ($g_{soll}$) gekappt:
$$
c = {g_{soll} \over g_{ist}} = {9 \over 18} = 0.5
$$
Wird auf eine Kappung der einzelnen Komponenten verzichtet (z.B. SMI), wird der Kappungsfaktor 1 verwendet.
Praktischer Teil
Nun wird es Zeit, die theoretischen Inhalte in der Praxis umzusetzen. Ziel dieses letzten Abschnittes ist die Erstellung eines Freefloat-Markapitalisierungsindex mit Hilfe des SimFin-Datenexportes SimFin-Datenexportes. Es wird davon ausgegangen, dass die bereitgestellten Marktkapitalisierungswerte mit Hilfe des Freefloat-Anteils berechnet wurden. Das nachfolgende Skript wählt die 30 grössten Unternehmungen dieser Marktkapitalisierung aus:
1 | # Total market capitalisation |
Der Ausschnitt beinhaltet nur die relevanten Zeilen aus dem Python-Code. Als Vorlage kann das Skript aus einem älteren Beitrag verwendet werden. Die einzelnen Komponenten des konstruierten Index setzen sich wie folgt zusammen:
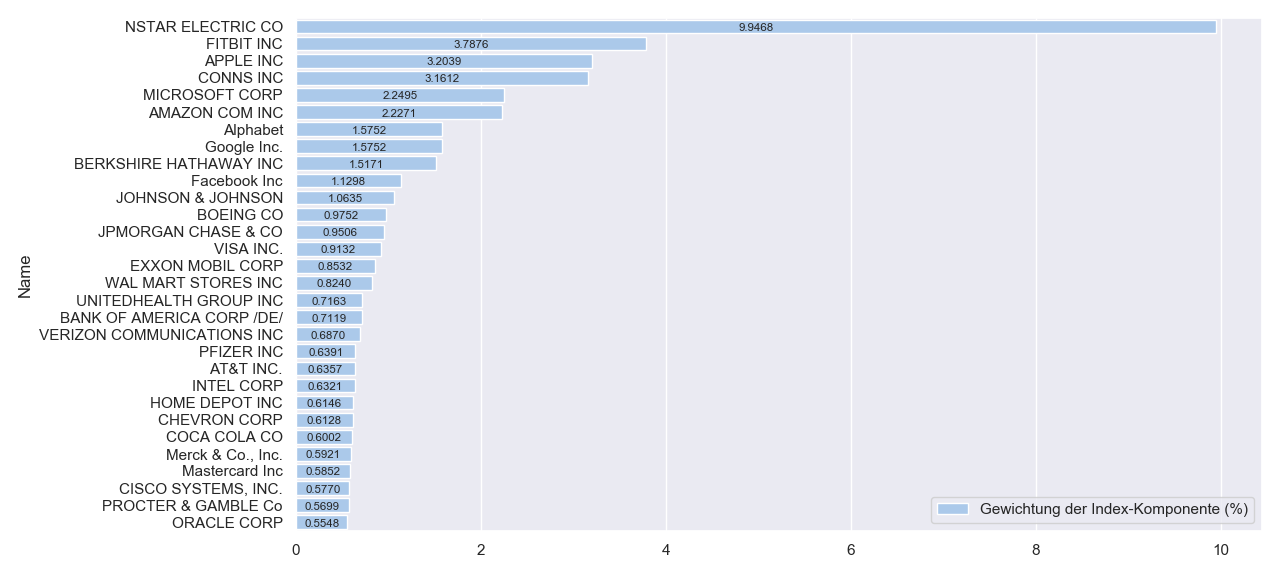
Wird dieser Index mit den Komponenten des MSCI USA5 verglichen (die Mehrheit der Unternehmen im SimFin-Export stammen aus den Vereinigten Staaten von Amerika), fällt folgendes auf:
- Die Mehrheit der einzelnen Bestandteile sind in beiden Indizes vorhanden
- Der Beobachtungszeitpunkt sowie die Datenquellen der beiden Vehikel scheinen unterschiedlich zu sein. Daher stimmen die Anteile (in Prozent) nicht überein
- Der Daten-Export beinhaltet falsche Kennzahlen (z.B. die Marktkapitalisierungen von NSTAR Electric, fitbit sowie Conn’s)
- 1.Seite des Bundesamt für Statistik zum LIK (inkl. Details zum Warenkorb sowie Formeln zur Berechnung des Indexwertes) ↩
- 2.Einfaches Beispiel (Workenkorb mit Bier und Pizza) von studyflix zur Formel von Laspeyres ↩
- 3.SIX Swiss Index - Reglement für Aktienindizes (inkl. Formeln) ↩
- 4.S&P U.S. Indices Methodology ↩
- 5.Liste aller MSCI Indizes inklusive der einzelnen Komponenten mit dazugehöriger Gewichtung ↩






